Power Analysis, Clearly Explained!!!

Stat quest is cool Stat quest .

Hello , I'm Josh Starman .

Welcome to Stag Quest .

Today , we're going to talk about power analysis and it's going to be clearly explained .

Note , this stack quest assumes that you are already familiar with what power means .

If not check out the quest , it would also be helpful if you understood the difference between population parameters and estimated population parameters .

If not check out the quest lastly , because we do a power analysis to avoid P hacking .

You should be familiar with that topic as well .

Imagine there was a virus and we had two drugs that we could use to treat it .

So we see how long it takes for three people using drug A to recover from the virus .

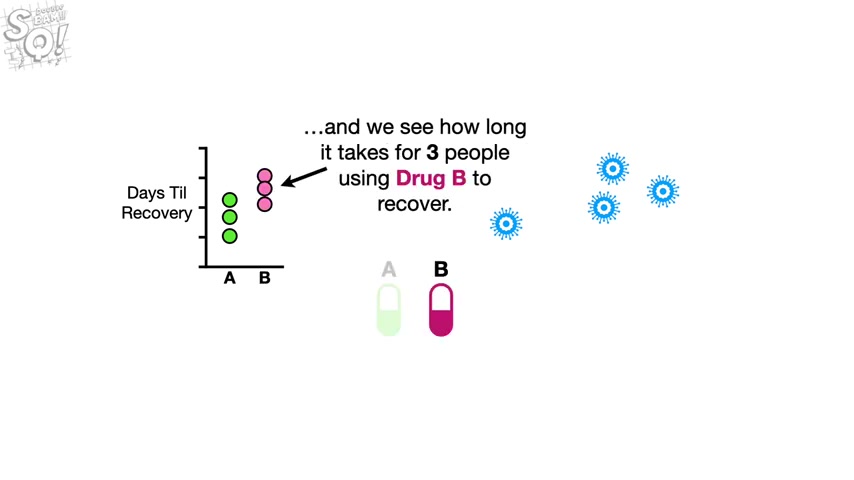
And we see how long it takes three people using drug B to recover .

Just looking at the data makes us think that drug A might be better since those people tended to recover from the virus more quickly .

So we calculate the means for both drugs and do a statistical test to compare the means and get A P value equal to 0.06 WW because the P value is greater than 0.05 .

The threshold that we are using to define a statistically significant difference .

We can't say that drug A is better than drug B .

In other words , even though we suspect that the measurements for drug A represent this distribution and the measurements for drug B represent this other separate distribution because the P value 0.06 is greater than 0.05 .

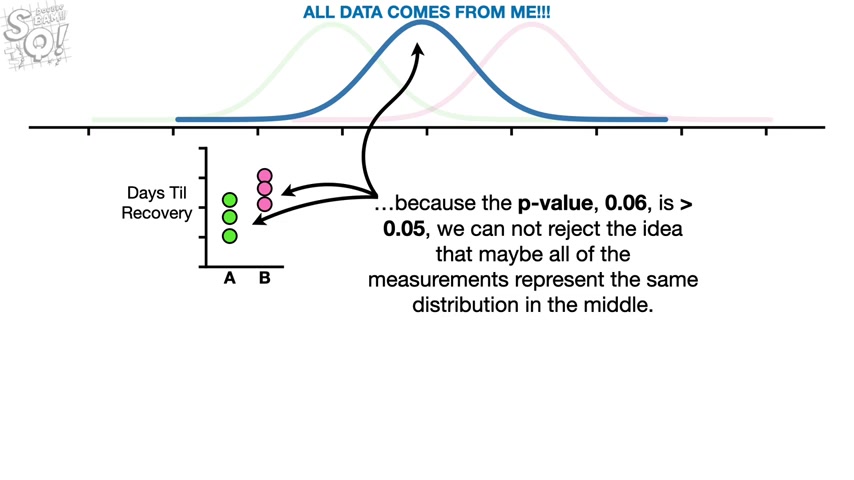
We cannot reject the idea that maybe all of the measurements represent the same distribution in the middle because we suspect that the measurements represent two different distributions .

And the P value 0.06 is just a little bit bigger than 0.05 .

It is tempting to give one more person drug A and give another person drug B and recalculate the means and then redo the statistical test .

However , we must resist this temptation because that would be P hacking .

And we don't want to do that instead of P hacking .

We're going to do the right thing .

We're going to do a power analysis to determine the sample size for the next time we do this experiment .

A power analysis determines what sample size will ensure a high probability that we will correctly reject the null hypothesis that there is no difference between the two groups .

In other words , if we use the sample size recommended by the power analysis , we will know that regardless of the P value , we used enough data to make a good decision .

Power is affected by several things .

However , there are two main factors .

One , how much overlap there is between the two distributions .

We want to identify with our study two , the sample size , the number of measurements we collect from each group .

For example , if I want to have power equal to 0.8 meaning I want to have at least an 80% chance of correctly rejecting the null hypothesis .

Then if there is very little overlap , a small sample size will give me power equal to 0.8 .

However , the more overlap there is between the two distributions .

The larger the sample size needs to be in order to have power equal to 0.8 to understand the relationship between overlap and sample size .

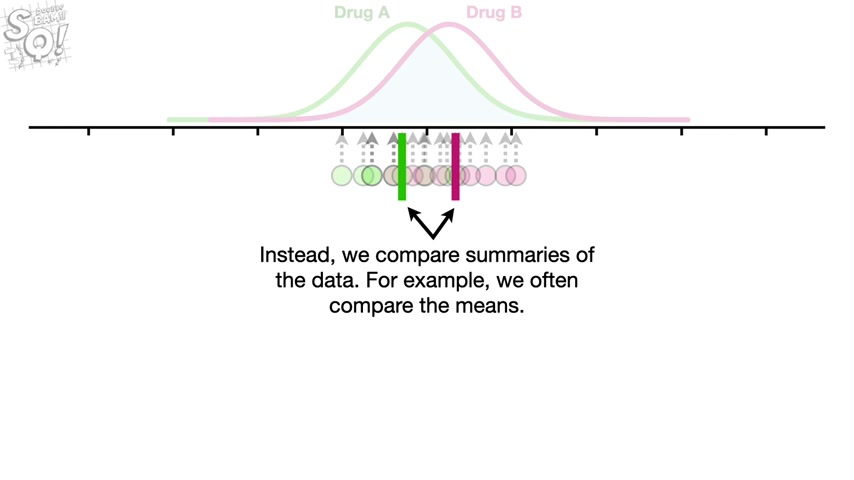
The first thing we need to realize is that when we do a statistical test , we usually don't compare the individual measurements .

Instead we compare summaries of the data .

For example , we often compare the mains .

So let's see what happens when we calculate means with different sample sizes .

First , let's focus on the distribution for drug A , the population mean for drug A is represented by this green arrow .

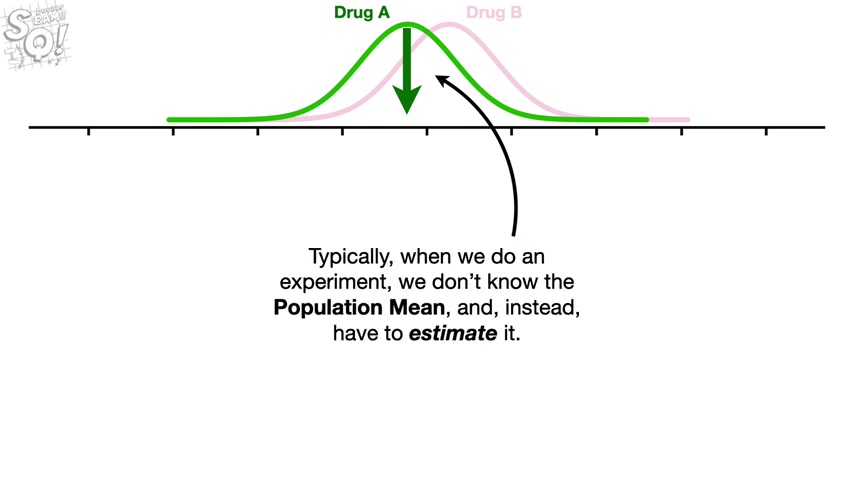
Typically when we do an experiment , we don't know the population mean and instead have to estimate it .

So if we collected one measurement and use that one measurement to estimate the population mean for drug A , then the estimated mean represented by this green bar would be the same as the measurement we collected .

Now let's get rid of the measurement , but keep the estimated mean and collect a new measurement and use it to estimate the population mean .

Now let's collect more measurements and use each one to estimate the population mean .

Note , we occasionally get a wonky point that is really far from the population maine .

And when that happens , the estimated mean is also pretty wonky and really far from the population mean .

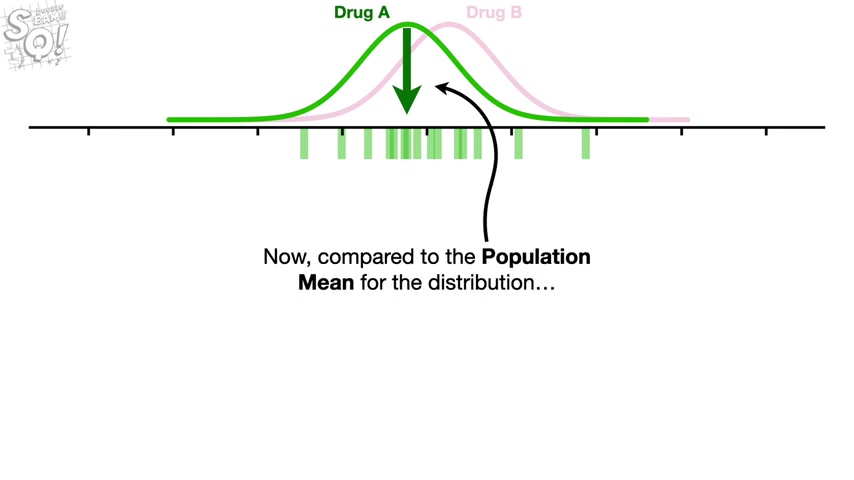
Now , compared to the population mean for the distribution , we see that the estimated means are all over the place .

In other words , there's a lot of variation in the estimated means and all this variation makes it hard to be confident that any single estimated mean is a good estimate of the population mean .

Sure , some of the estimated means are close to the population mean , but others are pretty far away .

And since 25% of the area under the curve is relatively far from the mean and off to the left , 25% of the measurements should be far from the mean and off to the left .

And since in this case , a single measurement is the same as the estimated mean , 25% of the estimated means should be pretty far off to the left .

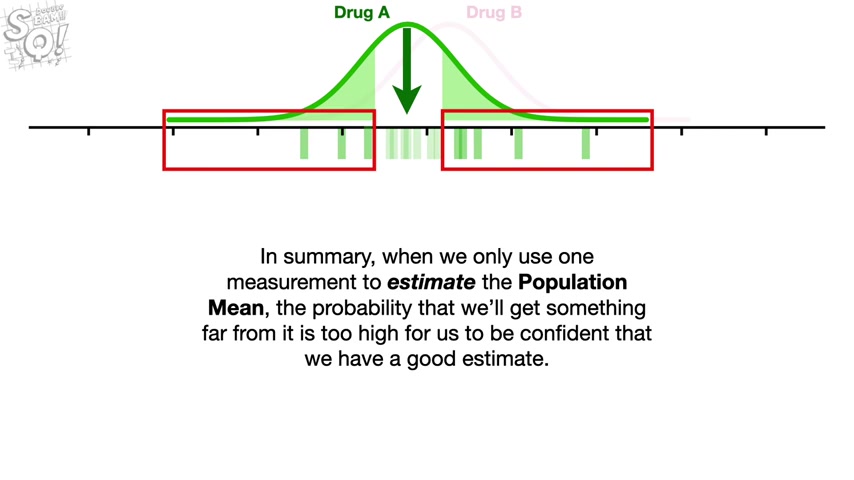
Likewise , another 25% of the estimated means should be pretty far off to the right .

In summary , when we only use one measurement to estimate the population mean , the probability that we'll get something far from it is too high for us to be confident that we have a good estimate .

Now , let's do the same thing for drug B collect one measurement and use that to estimate the population mean .

Now let's do that a bunch of times just like before compared to the population mean for the distribution .

The estimated means are all over the place and just like before , 50% of the estimated means should be pretty far to the left or right of the population mean .

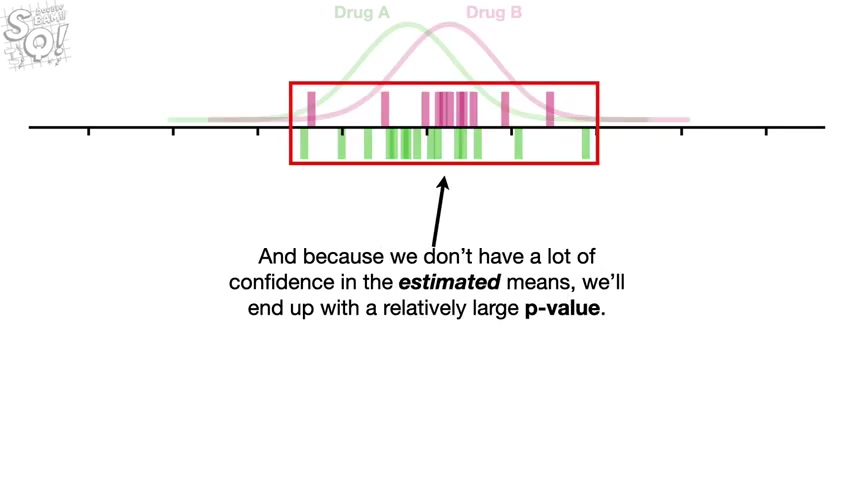
And when we only use one measurement to estimate the population mean , the probability that we'll get something far from it is too high for us to be confident in our estimate .

And because we don't have a lot of confidence in the estimated means we'll end up with a relatively large P value .

And that means we will not correctly reject the null hypothesis .

In other words , if this distribution said all data comes from me , then due to all of the variation in the estimated means we'd say in a small meek voice .

Dang , I can't reject the null hypothesis .

Bam .

Now let's collect two measurements at one time and use the average to estimate the population mean .

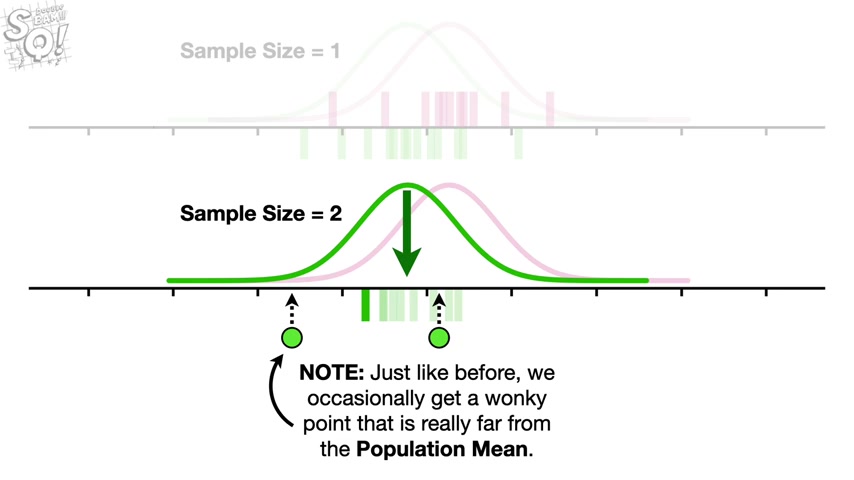
Now let's repeat that process a bunch of times , collect two measurements and use the average to estimate the population mean note just like before we occasionally get a wonky point .

That is really far from the population maine .

However , the other point we measured compensates for the wonky point and prevents the estimated mean from being too far from the population mean .

In other words , even though there is a 25% probability that we will get a measurement way out on the left side , there is a 75% probability that the next measurement will be in this range and pull the estimated mean back to the population mean .

In summary , when we use more than one measurement to estimate the population mean , extreme measurements have less effect on how far the estimated mean is from the population mean .

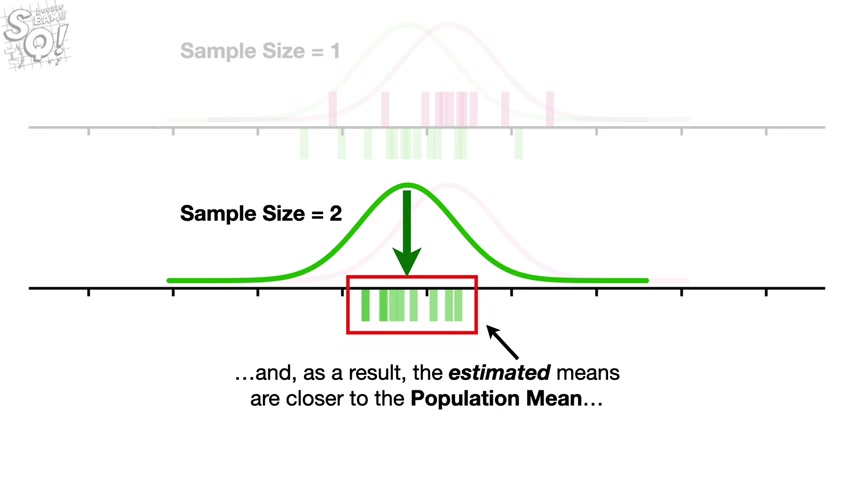
And as a result , the estimated means are closer to the population mean compared to the means we estimated with a single observation .

This suggests that we should have more confidence that averages estimated with two observations will be closer to the population mean than averages estimated with one observation .

Now let's collect two measurements each time for drug B and use their average to estimate the population mean .

Again , when we use two measurements , we can have more confidence that the estimated means are closer to the population mean compared to the means we estimated with a single observation .

Damn .

Now imagine we did the same thing only this time , we collected 10 measurements and use them to estimate the population mean .

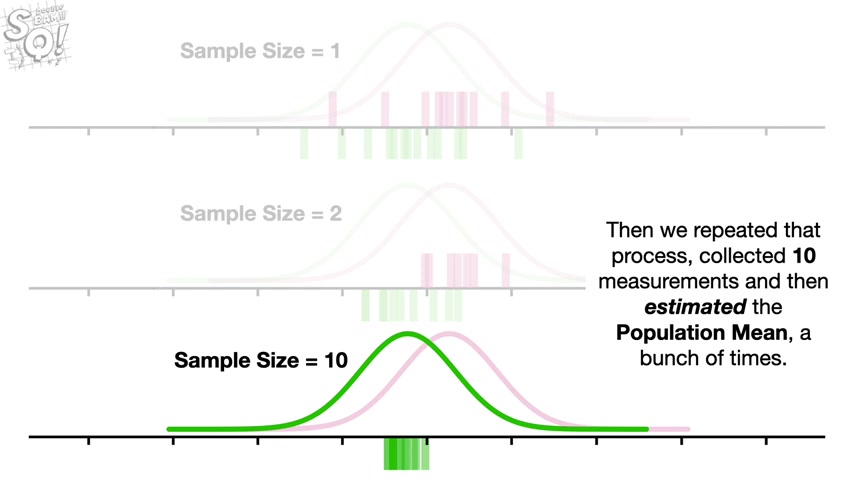
Then we repeated that process , collected 10 measurements and then estimated the population mean a bunch of times then we did the same thing for drug B .

Now we see that the more measurements we use for each estimate , the closer they are to the population Maine and the more confidence we can have that an individual estimated mean will be close to the population mean .

In this example , the estimated means are so close to the population means that they no longer overlap .

And that suggests there is a high probability that we will correctly reject the null hypothesis that both samples were taken from the same distribution .

In other words , even when the distributions overlap , if the sample size is large , we can have high power bam note .

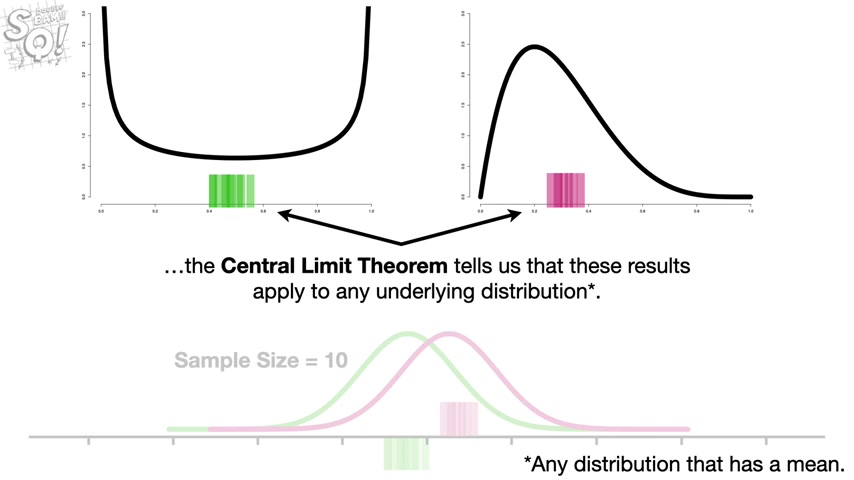
Although we used normal distributions .

In this example , the central limit theorem tells us that these results apply to any underlying distribution , shameless self promotion .

For more details about the central limit theorem , check out the quest .

The link is in the description below .

Now at long last , let's talk about how to actually do a power analysis .

First .

Remember that a power analysis will tell us what sample size we need to have power .

So the first thing we need to decide is how much power we want .

Although we can pick any value between zero and one for power , a common value is 0.8 .

So let's use that , that means we want an 80% probability that we will correctly reject the null hypothesis .

The second thing we need to do is determine the threshold for significance , often called alpha .

We can use any value between zero and one , but a very common threshold is 0.05 .

So we'll use that .

Lastly , we need to estimate the overlap between the two distributions overlap is affected by both the distance between the population means .

And the standard deviations .

A common way to combine the distance between the means and the standard deviations into a single metric is to calculate an effect size , which is also called D .

In the numerator , we have the estimated difference in the means .

And in the denominator , we have the pooled estimated standard deviations .

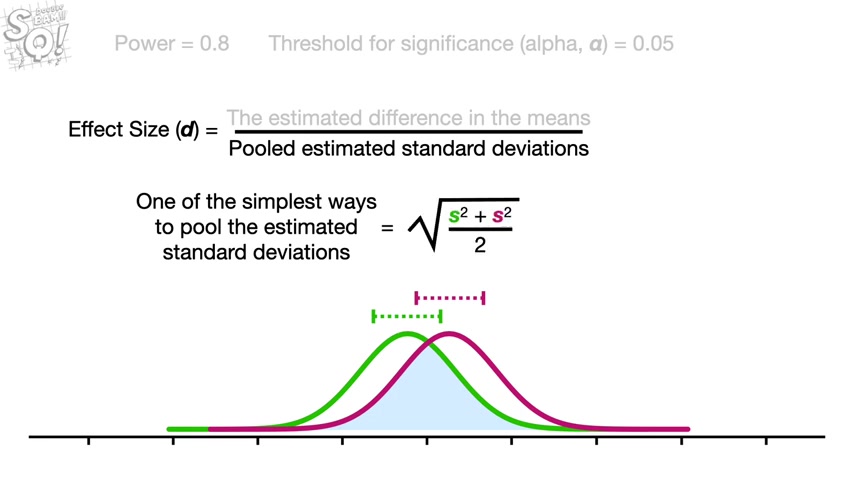
One of the simplest ways to pool the estimated standard deviations is the square root of the sum of the squared standard deviations divided by two where the green s represents the estimated standard deviation for the green distribution .

And the purple S represents the estimated standard deviation for the purple distribution .

Note , there are tons of other ways to calculate effect sizes and this is just one of them .

So when you do a power analysis , you may have to do a little research about how to estimate the overlap .

However , in general , the mean and standard deviations can be estimated with prior data .

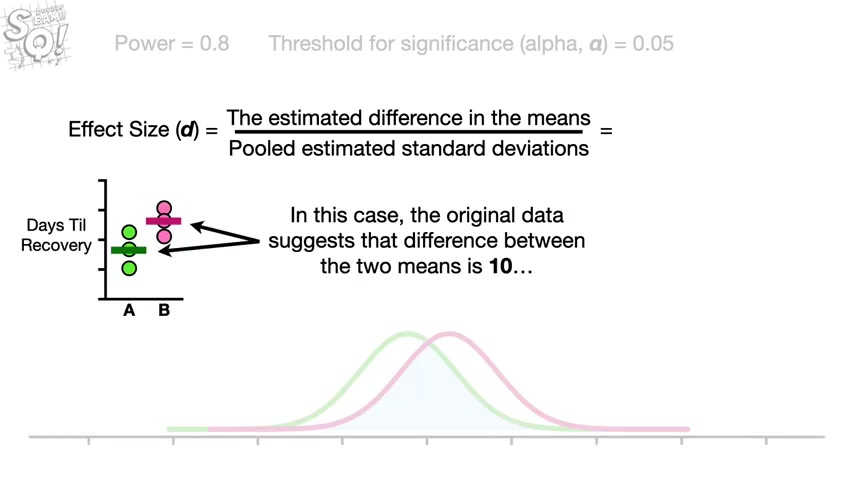
A literature search or in a worst case scenario , an educated guess in this case , the original data suggests that the difference between the two means is 10 and the estimated standard deviations are seven and six .

So we plug those into the formula for the pooled standard deviation and we get 6.5 .

So the effect size is 1.5 .

Once we know the effect size and the amount of power we want and the threshold for significance , we Google statistics power calculator .

Pretty much every statistics department in the world has one online .

Then we plug in the numbers .

I got sample size equals nine .

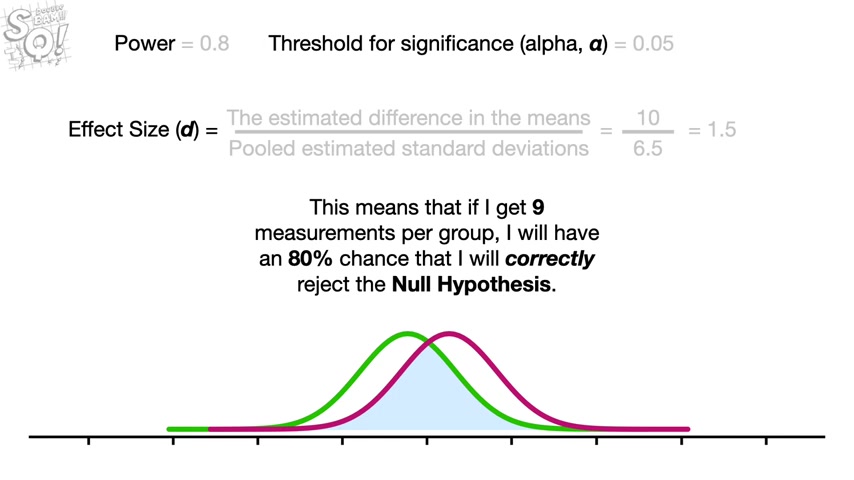
This means that if I get nine measurements per group , I will have an 80% chance that I will correctly reject the null hypothesis .

Double bam .

In summary , when two distributions overlap , we need a relatively large sample size to have a lot of power .

When the sample size is small , we have low confidence that the estimated means are close to the population means .

And that lack of confidence is reflected in a low probability that we will correctly reject the null hypothesis .

In contrast , when we increase the sample size , we have more confidence that the estimated means are close to the population means because extreme observations have less effect on the location of the estimated means .

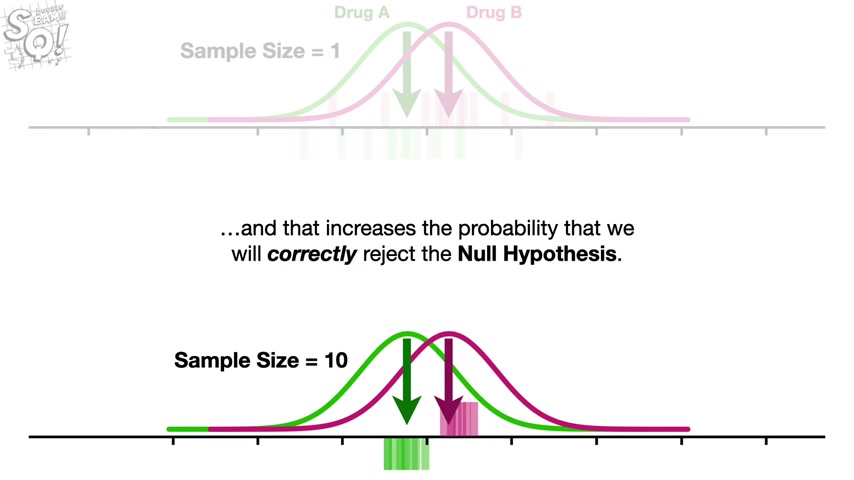
And the closer the estimated means are to the population means , the less the means from the different distributions will overlap and that increases the probability that we will correctly reject the null hypothesis .

And when you have a high probability that we will correctly reject the null hypothesis , you have high power .

Triple bam hooray , we've made it to the end of another exciting stack quest .

If you like this stack quest and want to see more , please subscribe .

And if you want to support stack quest , consider contributing to my Patreon campaign becoming a channel member , buying one or two of my original songs or a T shirt or a hoodie or just donate .

The links are in the description below .

All right .

Until next time quest on .