Attempting to Solve a PUPPET CUBE (With NO Help)

This cube may look like a simple two by two .

But watch this .

Oh Wait .

All right .

Check this out .

00 my God .

Make it stop .

OK .

Let's let's retrace our steps .

This is called the puppet cube .

And I actually unboxed this a long time ago thinking I was going to solve it soon , but then never got around to it .

Not because I'm scared by it or anything today , I'm gonna scramble and try to solve this with no help .

And if I manage to do it , then I will also try this one .

This is the puppet cube too and it can do way more stuff .

So I don't want to mess with this right now .

Sometimes before I start , I like to turn the puzzle a bit to try and understand it .

But I don't think I'm going to understand this thing .

So I'm just gonna keep turning .

Sometimes you can just keep turning around , but sometimes it will stop you if you bump into something like right here .

Clearly , there's nowhere left to go with this one bumping .

Wow , I'm really running out of moves here .

Can't even find a single turn .

I can do here .

How did I even get here ?

OK .

I actually don't know where I'm supposed to start .

I guess my first goal will be to try and turn it back into a cube shape .

That's what I did for square one .

So maybe it's gonna work for this too .

After all .

This is Puppet Cube One kind of want all the reds over here , but there's a piece in the way .

So how , how would I get that piece out of the way ?

Oh Man , I never deal with puzzles like this .

So I actually am just very confused right now .

I accidentally got a lot of yellow .

So maybe that's what we're doing now .

Um This , this looks like a two by two case where I want to twist it .

Who knows if that's even a possible thing ?

I'm literally just trying turns and hoping that they work because I have zero game plan right now .

I know I want to turn it into a cube shape , but I have actually no clue how that's gonna get done .

All right , I'm back to three yellow pieces .

I want to treat this like a two by two case .

Every fiber in my being wants to do rur prime right here to solve this .

Uh or maybe the other way you could solve it .

Come on turn .

Uh There's always something stopping me .

OK .

I know a third way and that sledgehammer .

No , I know 1/4 way .

L prime .

U two .

You oh , no , none of them work .

I can't get this yellow piece over here .

My two by two skills have failed me .

All right , we are back to turning randomly until some progress gets made on its own because clearly me thinking this through is not doing anything .

There we go .

There's a white layer .

What do we even have here ?

What that worked ?

Oh , I'm a genius .

We're gonna try and solve the rest .

Um How does this even work ?

Actually ?

No , I have a better idea .

It's solved .

All right .

Uh These things they like don't turn on their own .

What I'm thinking is I'm gonna need algorithms that keep all the corners where they are and move these center pieces around .

I wonder if something that I do want a two by two that just keeps all the pieces in the same spot could move these around .

For example , if I do um sexy move six times , huh ?

Doesn't look like that's possible , at least from this angle .

Oh no .

Come on , please reverse uh like a soon and then an anti soon somewhere else to solve it .

Uh I can't tell which algorithms are possible and there's a lot of different ways you can hold this thing which make different things possible .

Like this one , for example , blue top white front .

If I try to do this stops on , move three .

But if I hold it over here stops on , move four or five .

That means if I try algorithms I already know and see if they work on this cube .

I'm gonna have to try it from many different positions .

Guys .

After so much trial and error , I finally found an algorithm that does nothing to the two by two corners but actually affects the inner pieces .

That algorithm is this um And then that , so that might seem a bit random .

How would I even know that that doesn't move all the corners around on a two by two ?

Well , this is just the U perm or three edge swap on three by three , except with the setup moves taken out .

And since the algorithm only swaps edges , then it doesn't actually do anything on a two by two .

Here it is on a two by two .

It always looks really funny .

All right .

Now that I've found an algorithm , I need to figure out what it does to see if it can be useful to me .

For example , let's focus on the bottom right here .

I'm going to do the algorithm once .

Uh And now it's a different color .

So I'm gonna do this algorithm again and see where this piece goes .

So let's track it .

I can still see it .

Um It's still 00 no .

Oh It's been hidden .

All right .

So it went over there .

What the heck .

Oh This is annoying because the pieces are gonna keep disappearing .

Do I need to map out every single piece .

All right , I'm back .

I did some testing with that algorithm and I've figured out how to make some progress .

So I'll show you what I did notice that this is white , red and blue .

These three are going to stay where they are when I do the algorithm and these three are going to change .

So we have a green , green , orange and now we have white orange , blue , these three have not changed and the other three have all changed .

Also fun fact , since this algorithm doesn't affect the corners , I can start it from anywhere in the algorithm and it will still not affect the corners .

If you try to start the algorithm from move 1 to 6 , six or seven , it just doesn't work .

The cube gets stuck .

So if you start it from any of the other points , it preserves a different set of pieces .

This is really useful because now I have six different algorithms for the price of one .

I wonder if blue top red front will work .

Let's just give it a shot .

Yeah , it works .

There are so many possibilities of what this algorithm can do .

And I really hope that this is enough because if I need to come up with another algorithm , I'm going to be very angry .

All right , let's try to make some progress .

I don't even know what I'm doing , but I will talk through how I'm thinking .

The fifth version of this algorithm preserves this one , this one and this one .

So I just want the red one to be preserved .

Let's give it a shot and see if any other pieces get solved .

All right .

That didn't work .

If you do it five times it comes back to normal .

So I'm just gonna try it again .

All right , great .

We got an extra piece solved .

Now , I'm looking at my list again and if I want to preserve these two , I need to use the third version of the algorithm .

So let's go ahead .

All right .

I don't think any other pieces are getting solved by this .

I can't guarantee any other pieces get solved when I do this because I only wrote down what doesn't move .

I didn't write down how the other ones move because that would be a lot of work , but it would probably be useful to do that .

I'm just , I just haven't done that yet .

Guys .

I am having so much trouble figuring out what to do next .

I tried to make more algorithms but I could not come up with any .

This cube is just so restrictive .

You know what ?

It's getting late .

Maybe I'll continue this tomorrow .

All right , guys , I am jealous of you .

Probably just sitting in the comfort of your own home watching this thing because I just spent like five hours last night on this .

It is the next day and I think I have a way of solving this .

I came up with a pretty solid method of how to solve the rest of the pieces .

And in fact , not just these six pieces because there are nine pieces on this thing in total nine of these pieces , which I'm gonna call edge pieces .

These are actually they look like center pieces , but they're edge pieces .

How this cube works is that there is an internal three by three which you can kind of see here .

So if you look at it like this here is where the three by three is located , except it's not quite a three by three because it's missing some pieces .

This corner is so big that the three edge pieces here they don't exist .

Instead , we have 123456 visible edge pieces and we have three hidden edge pieces .

The three hidden edge pieces are over here here at the bottom left , there's one here at the back left and there is one at the very bottom back .

So there are nine edge pieces in total on this cube .

I'm going to try and solve all of them .

I'm sure you can just solve the visible ones or even not solve them but have them as the correct color and have a wrong side color .

That would almost make this thing look solved .

But since I found a method that could actually solve every piece , even the hidden ones , then I think I should just try and solve all of them .

So remember how I was talking about that algorithm that I found , which goes like this plus all of its variations .

Well , it turns out this does a five cycle of pieces .

And what that means is it takes five pieces and it just moves them all into another's location next to each algorithm I also wrote which visible pieces it preserves .

So next to the first one , I wrote a Lo .

That's because using my blindfolded letters , this is ad klno and A LO means A L and O do not move when you do this algorithm .

Then next to that , I also wrote the cycle of pieces that it does .

The first one does a cycle of Duwnr .

And so this is D this one is U so I know that the orange of the orange , green is going to go to you , which is the bottom facing part of this after I do the algorithm and there it is and whatever was here is going to go to W and whatever was here was going to go to N and so on .

So I had that written down for all six algorithms .

And then I also found two more variations done from different angles that can also be used as algorithms for a total of eight .

Now those algorithms work with red top , yellow front .

But as long as you have the red , yellow , blue corner , what I call the pivot corner in the same spot .

Like this .

For example , then all the algorithms still work but they will affect different pieces because I've turned the whole cube .

So my eight algorithms became 24 algorithms and that's not it .

If you have a five cycle algorithm , you can do it 123 or four times .

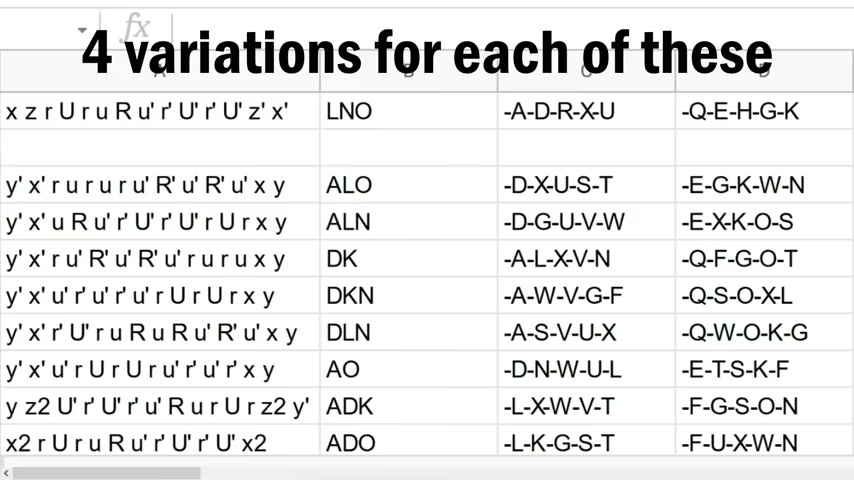
And those all work as different algorithms , there are four variations to every single algorithm I came up with for a total of 24 times four or 96 different unique algorithms .

Now , on the bright side , I don't have to write 96 different algorithms .

For example , if we look at the first one , if I did this algorithm twice , I would just go through every second letter instead .

And that would be DWR UN anyway , this was getting so complicated .

And I spent hours just on writing out the algorithms because I , I guess I had so much faith that this would somehow work in the end .

Even these 96 algorithms I realized that I probably don't have the algorithms I need to solve this thing .

So I did what any sane person does and started combining these algorithms randomly to see if I could come up with anything useful .

And I did if you combine this algorithm with doing this algorithm twice , then you get another five cycle which turns out is very useful because it preserves for the pieces .

And I found out if you do this algorithm followed by this algorithm and then do it twice , you get a two flip , just two edges flip and this is huge .

I don't know if you guys understand how important this one is .

If I didn't discover something like this , I may still have doubts about being able to solve this thing .

But this , this is just so good .

So I'm going to talk a bit about why that's so important later .

But first , I need to show you the method that I came up with for how to solve the rest of this .

The first step is just to solve any piece .

And I decided to go in a specific order .

So I'm going to solve the K piece first .

Remember it's ad klno .

I'm going to be naming them with letters .

But any time I say it , I also point at it .

So you'll know what I'm talking about .

So let's try this .

I want to solve the K piece .

This is the yellow orange and I need to go around finding that thing because I do not see it right now .

Oh I found it .

OK .

It is over here .

I need the yellow of yellow orange .

So that is the one right here , which is the letter H .

So I need H to go to here , which is K .

All right .

Let me just quickly scour through my 96 algorithms .

I found this one which has both H and K in its cycle .

They are two steps apart which means I will have to do this algorithm twice and then K should be solved .

So I'm bringing H over to K in two steps .

Let's do this .

So Xy , and then the algorithm and again , hey , sweet , I got it .

I also got this one , but that's not going to be the one that I try to solve next .

So we're going to ignore that one .

When I looked through my algorithm list , I noticed that the combination of DK and N actually showed up a lot together .

So I'm going to solve these three first .

So the next step is to solve D but I have to preserve K .

I can't let this one get unsolved .

Let's quickly search for where this piece is .

So this is the red green piece .

Is it that nope , it's this one .

So this is the letter T and T needs to go to D .

So let's go see if I have an algorithm that does that .

This is the boringest part just going through looking for algorithms that do what I want it to do .

Here .

There is one that has D and T and preserves K .

So we can use this one .

I need T to go to D , which means I need to do this algorithm twice backwards or three times forward .

I don't want to mess it up .

So I'll just do it three times forward .

So here we go X prime Y prime and then the algorithm And then again , I'm always scared , I'll mess up when the cube doesn't turn .

OK .

Third time .

And let's see it .

There's D correct .

K is still correct .

All right .

Next we're gonna solve N .

So we need an algorithm that preserves D and K and involves N in some way .

Let's go look for where that piece is .

This is uh the blue of blue white .

I have found blue white right here .

So I need this one .

This is the letter V .

I need V to go to N .

All right , found one here .

This one preserves D and K and has V going to end in just one step .

So here we go , Y prime X prime .

I'm just realizing the amount of trust I'm putting into my algorithms is gigantic .

But all right , here we go , DKN .

Let's go .

These three are solved .

All right .

Now , I am down to using only algorithms that preserve DK and N I'm gonna start by tracing right here .

So this is the white orange , which goes to the white side of white , orange .

Um This is blue orange and that goes here .

The letter here is A A goes to S which goes to O this is white green .

So that goes right here and this is R which goes back to here , but on the flip side and then uh we have L here which goes here and uh yeah , it goes back to the flip side .

So we have actually two different cycles here .

And what we're looking for is just 15 cycle .

So what I'm gonna do here if I don't have what I want , which is just 15 cycle is I'm going to just do one of the algorithms I have randomly that preserves DK and N and see if that gives me something better .

So I'll try one of them here .

All right .

What , what the , what ?

OK .

That's solved a lot .

Um It solved this one and this one , but that's not actually that useful because here we have one here , which goes here , which goes here , I have a three cycle and I don't even have a way to do that .

So I'm just going to try that again and hope if I end up with a five cycle .

OK .

I ended up with a four cycle and two cycle again .

You see how difficult this part is .

I'm basically just trying stuff that preserves these three , just keep moving the other pieces around until I end up with a five cycle .

And even if I do end up with a five cycle , it's so unlikely that it matches any of the algorithms that I already have .

OK .

This is exciting .

I've set up something that I think I can solve .

I did some random five cycles that don't affect the pieces I've solved .

And I managed to get 1234 in the correct spot .

These I label ad K and N I have an algorithm here that preserves those four pieces .

The algorithm that I'm using can only solve these four specific cycles .

So let's see if what I have on the cube matches any of those cycles we can start here .

This is the letter L and then this is green of orange , which goes to this spot and the green side , this is G , then this one goes to here , which is S this one goes to here , which is H and this one goes over here , which is O and it comes back to the start .

All right .

LGSO does not match any of the cycles that I can do with this algorithm .

I have four algorithms but there are 384 possible cases that can occur here .

This gives me a 1% chance of solving the case that I have .

But now let me tell you why having a two flip algorithm is so important right now , I'm saying that this L since it's green , it goes to the green side of green , orange .

And that is the letter G .

But the opposite side of this piece is the letter X .

Now , if I don't care about the way the pieces are flipped because I can use my two flip to fix that all at the end , then I don't have to worry about which side it ends up on .

So here is my original lettering scheme for the edges and I will go through it again .

But with a simplified lettering scheme where every piece only has one letter .

Now this is still L , this is X , this is W , this is R and this is V and I will also rewrite the cycles that my algorithm can do using this simplified lettering scheme .

Would you look at that ?

We have a match ?

Now , I did get lucky because this algorithm doesn't cover all the cases .

But because I have the two flip , there are actually only 24 or possible cases which gives me a 17% chance of being able to solve any case that I get .

Now , 17% doesn't seem great , but I only need to solve the puppet cube once .

So I will take this 17% all the way to the bank .

So I am going to do this algorithm twice and it's going to put all the pieces in the correct spot but not necessarily flipped correctly .

I really hope this works .

All right .

So I start with the XY and then do this and then uh go back to the beginning and do Y prime X prime and do this .

Oh My God .

What happened ?

Now , I'm back to the beginning .

Wait , this is the beginning .

OK .

Now Y prime X prime , I gotta be more careful and do that again .

OK .

Now I've done the algorithm once I need to do it again .

Back to red top , yellow front .

Which is my default .

And we're going to go again .

So Xy and go back to here and go Y prime X prime .

And the last part of the algorithm do this twice right moment of truth .

Uh This is in the correct spot .

This is green and yellow .

That's great .

This is orange , blue , it's in the correct spot .

All right , I just need to check that every other piece is actually solved .

So this Oh My .

Oh yes .

Everything on the inside is actually solved except for these two .

OK .

OK .

This is progress .

So now I just have this piece and this piece flip and I need to flip both of them .

And I have a two flip algorithm .

The only problem is it only flips two specific pieces and that is the A piece over here and the W piece which is back here .

However , this should not be a problem because I can just set these two pieces up in that spot and then I can flip them both .

But first , I'm going to do this .

Now , one of them is already in the A position .

I just need this one in the W position over here .

So I need an algorithm that takes a piece from L moves it to W and doesn't disturb the A piece because this needs to stay here .

All right , I found an algorithm .

This one does LXWVT and doesn't touch the A piece L and W are separated which means I just have to do this algorithm twice in order to get L over to W .

So this one goes YZ two and then this and I just have to do it twice .

So I'll do it again .

All right .

Uh Let's go back to yellow blue .

So this is still here , flipped and the W position holds my orange blue piece nice .

Now , I just need to flip them with the flipping algorithm that I found .

All right , better not mess this up .

This one goes like this uh one algorithm without a rotation first and then Xy this and then go back to the beginning .

Do this again because I have to do this algorithm twice to flip it .

And the last part again um oh that flipped .

OK .

I probably did it correctly .

This orange blue still here .

It probably also flipped .

So now I have to undo the setup of five cycle that I did .

So I need to get everything back .

So that's gonna be YZ two and this at once .

That's twice .

OK .

Here we go .

Moment of truth .

Oh Yes , I have to check if it's solved , but it looks solved to me .

So there's one right here .

Nice one right here .

Good .

And the last one was right here .

Ah Beautiful .

I have solved the puppet cube .

I spent so much time on creating a method for these six pieces that I don't even remember what I did to turn .

It into cube shape , but I am not solving this thing again .

Oh No , there's still the puppet Cube two .

Wait now that I understand the puppet Cube one .

I feel like I feel like this would be easier because you can just turn some of the edges without turning anything else .

OK ?

We're scrambling I think as I scramble this , I'm supposed to throw in some sliced moves sometimes , but like I can't even figure out the finger trick to do it .

OK .

Again , I'm trying to make cube shape .

Uh Let's hope this is easy .

I've got most of it already .

Nice scramble .

Some might say I cheated but I did not .

All right .

Wow , that was so easy .

I feel like I should just res this but I am not going to , I'm just gonna solve the rest of it .

Can I do commutators ?

Hang on ?

OK .

This , this goes right here and this one goes right here .

OK .

Let's just give this a shot .

I don't know if this is if the moves I'm trying to do are going to be accessible to me as I do them .

Um That should know .

OK .

What about this ?

OK .

I slice first and then um do this doesn't look like that's oh What , what , what did I just , I just accidentally did an extra slice move here but like I solved this one , I solved this one and I had solved that one .

I just messed up a slice move .

So if call me theaters work , then this is gonna be so easy .

All right , we are down to our last algorithm .

This one goes here , which goes there .

This is so funny .

It's so funny that Puppy cube two is easier than puppet cube one .

We're gonna move this one over here first with rur prime .

So ru our prime and then oh no , I can't see anything .

OK .

I think we do this slice move .

Oh And then we're gonna do a reverse .

So our U prime , I'm like smiling really hard right now our prime and then I actually did it .

I did the puppet Cube too .

I did not expect to be doing this in this video .

We're gonna slice through every side just to make sure it's actually all solved .

Wow , guys for Puppet Cube two , all you have to do is learn three style and have a little bit of patience .

Turns out all along puppet Cube one was the real final boss .

And yes , since this is just a normal three by three , you can take it apart like a normal three by three edges first and then corners .

And there is a normal three by three core on the inside except for this giant corner which is just attached to the core .

If you have your own scrambled puppet Cube , I think your best shot at solving it is probably just by taking it apart .

I do not recommend trying to actually figure this thing out .

And when you reassemble it , you want one of the visible edge pieces to be your last one .

So it's a little easier to snap in Puppet Cube one is by far by so much the hardest puzzle I have ever solved .

I'm sure there are much harder ones .

But Puppet Cube One already made me angry .