L-2.2 - Reflexive Relation with examples _ Discrete Mathematics

भीवान्ट लिएम्स बार्ज यहाँ पाज करते हैं। इस विडियो में यहाँ जाएरे हूँ , रिफ्लेक्सिव रिलेशिन् और बीलकुल बेसिक से इस्तार्ट करूगा यहां इजाम्पल के साथ ताकि आपको विवान्ट काई जीस्ट्रिर्दियां , पराइकिकारिज आप इसीली आंस्वर कर सकते हूँ तो वाईज फ़ड़ाइ विड़ीओ को लाईक कर देना जैनों को सभश्क्रब करना अगर इप दिखा नहीं किया और अगर कर भी दिया है और डिवाइसी से सभश्क्रब कर वा सकते हो सभ्श्क्राइबर्स बहुत ज़ोरी हैं त आपको लास्ट वीडियों में मैंने बताई हूआ हैं , कार्टीसम प्रटक्ट के बारे में बताई हूँ हैं तो अब रिलेशन के अंतर नहीं जब हम बाइनरी रिलेशन की बात करते हैं तो उसमें आते हैं हमारे पस दिफ्रेंट दिफ्रेंट आगे प्रॉपर्टीज � if a relation r on a set a is set to be reflexive , if x , x belongs to r , for every x belongs to a .

बद्लाक कहने का ये देखो दिखने में आपको लगरा पटनी क्या देदिया .

लेकिन सिमपल सी भाशा हैं अगर मैं आपको बता हूँ नहीं .

if every element of a set is related to itself then it is a reflexive .

elements आपको दिए होगे हैं , अगर set के अंदर सारे के सारे elements खुद से ही क्या हो रिलेटिट हो , खुद से आपसमें नि , खुद से जब रिलेटिट हो , then it is called a reflexive relation .

तो वही यहाँ पे लिखा हो हैं , मतलब आपको वो सारे pair उठाने हैं , वो सारे के सारे पेर उठाने हैं जिसके अंदर x,x हो , x,y नहीं होना चईए , मतलब कहने का कि कौमा के इस तरफ लग वैल्यो और इसर अलग नहीं दोनो तरफ सेन वैल्यो ही होनी चाहिए , ये आपको यहां पे उठाने हैं x,x बिलांग स्� होनी चाहिये। ये आपको यहाँपे अथाने हैं। x , x belongs to r for every .

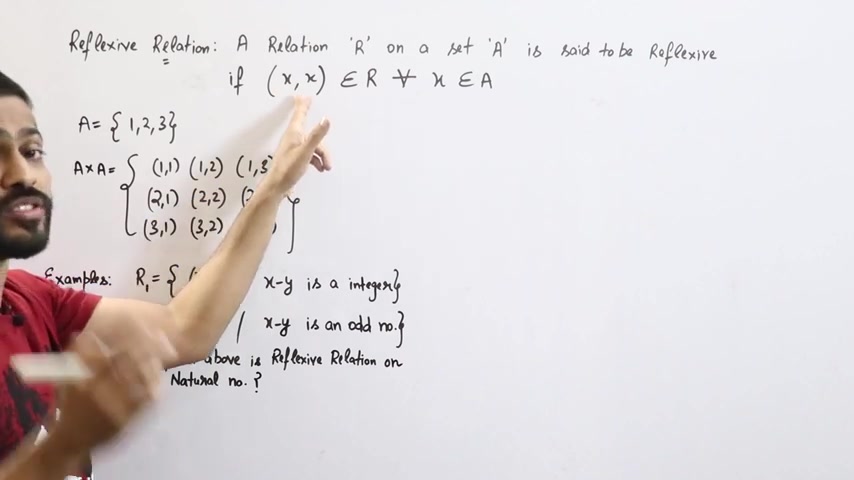
मदलब आपको सारे के सारे वो पेर उठाने हैं। जो उस सेट के अंदर आते हैं। और उस सेट के अंदर हरेक आलिमेंट अपने आप से रिलेटिड होना चाहिए। यह लाइन चाहे हिंदी में लिखलो अपने नोट्स में लेकिन नोट्ट कर ले ना बहुत इंपूर्ड़ेंड लाइन हैं। मेबी आपको यहाँपे अभी समझ आ जाएं जब आप इसके एजम्पल करोगे ना लेटर उन बहुत सार एज आपको ये लाइन जो है वो बहुत हल्प करेगी और क्या आपको अज्टाल है आपको आपको आपको आपको कालादादार। आप देखो मैं इसको आपको विद एक्जामपल बदाता हूं लेट से मेरे पास सेट आई जिसके अंदर ओंदर दू त्रीज़्ान त्रीन आ मैं सब सब से पैले क्या करूका। अवैस्छी अबिप तो रेलाशन के पर संगर गाईरेंमांगां के लिए मिर को ख्रॉस्परॉडक्स कीआं। मदलब आप कई सकते हूं कार्टीजन पॉटक्ट कीया , एक आईके साथ कार्टीजन पॉटक्ट कीया .

तो जब हम कर 3 का विथाया है सब से cross multiply करके हैं हमने 9 elements लिख दी हैं विथाया पॉर्ट ?

तो मेरे relation में जो मेरा relation है normal जो relation और binary relation उसमें इनमें से कोई भी आप विथा सकते हूँ पूरा का पूरा भी विथा सकते हूँ इत is a subset of this cartesian product लेकिन अब अगर मुझे उस relation को reflexive relation विनाना है जहां पे खुद से वो रिलेटेड हों मतलब एक्स कोमा एक्स वाला उठाना है यानि कौन सा उठाना हुँगा ?

वान कोमा वन कौन सा ?

तू कोमा तू कौन सा ?

तू कोमा तू गेडिंग तो पॉइट और नौट ?

मतलब आप सारे दाइगनल एलिमेंट से इस तरीके से उठालोगे ब्कौस x,x दिख रहा है न ?

इदर भी x , इदर भी x मतलब 1,1,2,3,3 तो यह एक्चल में आता है रिफ्लेक्सिव आप नॉर्मर रिलेशन में तो इन में से कोई भी सेट ले सकते हूँ लेकिन अगर आपको रिफ्लैक्सिव रिलेशन बनाना रहा नहां तो आपको 11 , 22 , 33 लेना ही पड़ेगा .

वादा पाइट राजा या नहीं पाइट राजा या पाइट रिलेशन आप बोल सकते हूँ .

लेट सी अगर मैं एक ओर लेले है बड क्या ये रिफ्लैक्सिव है ?

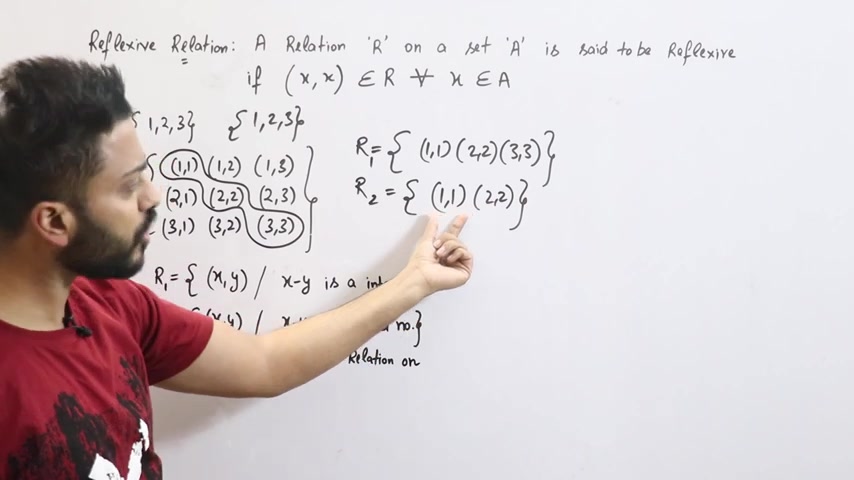
नहीं दिखने में आपको लग रहा हूगा कि हां जी सर x,x के पॉइट अवू से 1,1 भी आगया , 2,2 भी आगया लेकिन गाईस , पर एव्री x ब्लॉंगस तो a , पर एव्री x मतलब 3 का हैं ?

वन के प्रीज़ तीक है , तू के प्रीज three काहें ?

one के according थीक है , two के according थीक है ?

लिकिं 3,3 यापे नियाआ .

means it is not a reflexive relation .

सारे के सारे elements अपने आप से related होन चीएंयेते हैं , सारे के सारे get the point or not .

क्योंकि ये बड़ा important point है .

ऐसी अगर मैं एक हौर लिगते हूं , let's say 1,1 , 2,2 , 3,3 और कि एक हौर लिएल यह अपने प्राइंट पॉईट है। ऐसी अगर मैं एक अपने लिख देता हूं , लेट से 1,1,2,3,3 और लेट से और लिए लेते हैं योई 1,2 .

तो क्या यह रिफ्लेक्सिव है ?

हां यह भी रिफ्लेक्सिव है , अब आपके दिमाग में आ रहा हो गया है कि सर वान वान , ट� अब आपकी दिमाक में आगगा कि सर तो थीक है लेकिन यह वन टू आगआ .

वन टू के इडर तो इकस है इदर वाये है। मतलब ये दोनो तो बराबर नहीं है। यह एकस एकस तो नहीं है .

कौई दिकत नहीं है .

हमारा रिफ्लैक्सिव रेलेशन क्या कहता है ?

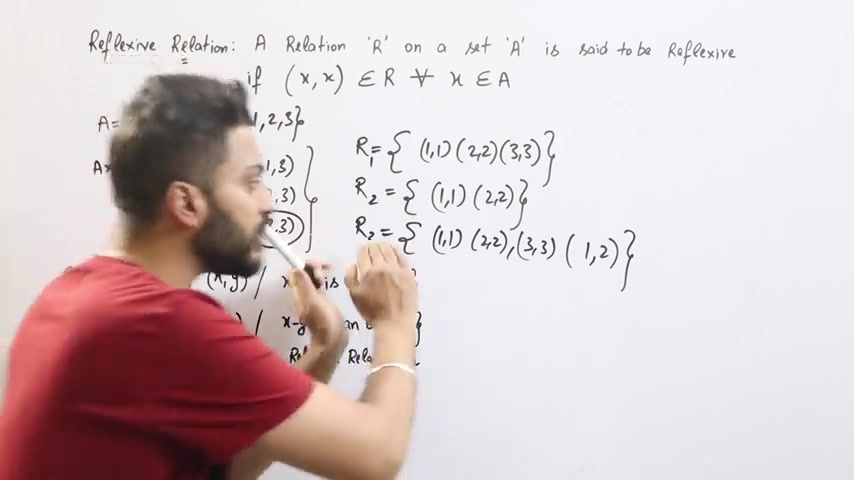
शकत है य पुरे में से कोई भी उठा लो। लेकिन ये तीन आयंगे ही आयंगे .

358.64 --> 433.5426

लेकिन आपको कहीं बर exam में इस तूरीके से भी अलग टाइप में भी question आ जाता हैं .

जैसे relation हैं r1 , x , y हमें इस तूरीके से दिरक हैं , x , y y , x-y is a integer .

यहाँ पे मेरे को दिरक हैं , check which of the above is a reflexive relation on a set of all natural numbers .

मतलब मुझे natural numbers उठाने हैं कोन से दो ?

x और y मेरे कोई भी दो natural numbers उठाने हैं .

और अगर मैं x-y करता हूं , मैंने को कोई pair उठाने हैं , उस pair में एक x हैं और ए अगर मैं अक्स मैंस वाय करता हूं , मैं वे तो कुई पेर उठाना हैं , उस पेर में एक एक वाय हैं .

गेटिन दे पाइर्ट रूड़ ?

एक एक वाय हैं और वो मुझे नाच्रल नॉमबर में मेंसे उठाने हैं और जब मैं x माईनस y करूगा तो आनस्वर इं टीजर आना चाहिए क्या ये रिफ्लेक्सिव होगा या नहीं होगा तो देखो आपको इस तरीके का कॉशियन कैसे करना हैं बढ़ा द्यान से देखना चेक विच्योद ते फॉलिंगींज ये र on all set of natural numbers .

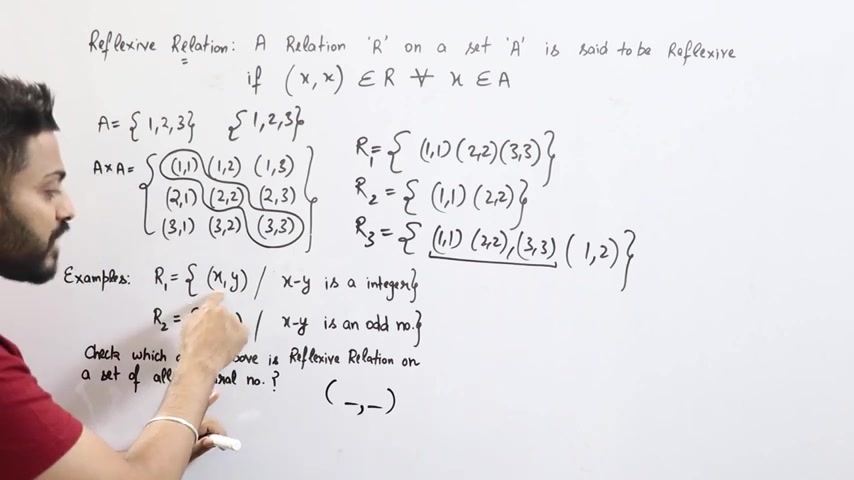
सब से पहले आपको आपको , x और y की वैल�анов नहीद उठाने हैं .

let's say मैंने , x की वैल� georgian value of 2 नहीद उठाने है , तमस्नुम्ह है , तमस्नुम्ह वैने उठाने है , आप दिको , सूब कोज़र से वाक्षिश के वैल�세 , तो कहींउं के दमावी में आयेगा कि सर y की वैल३ , तमस्न अंजर y की वाल्यू लेट से में ले लेता हूं 3 लेटीन देख देख पूईण ?

अब मैंने क्या किया ?

x-y किया x-y 2-3 किया अंसर क्या है ?

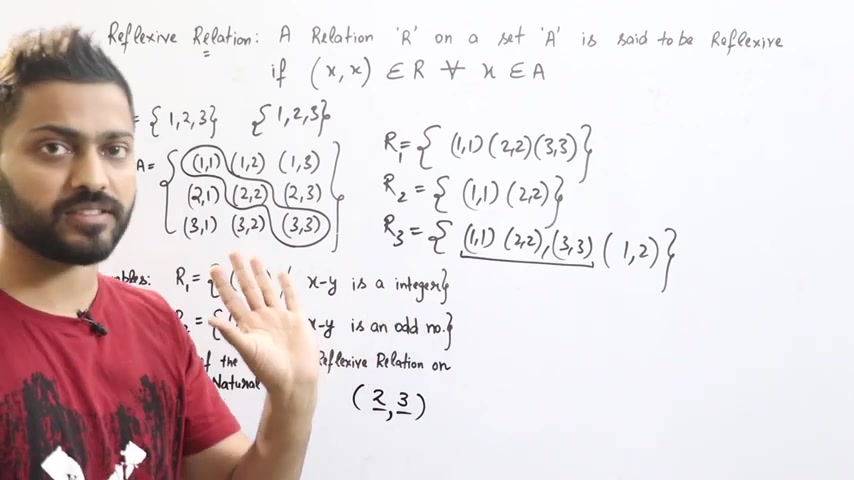
माइनस वं इतिजर येस आपके दिमाइमें ये भी आ सकता है लेकिन गाईज , यह गलद त्रीका हैं साल्व करने का क्यूं ?

आपने एक्स की वैल्यू तू डाल दी ?

तिक है जी , नच्रूल लंबर है लेकिन मैंने आपको क्या बूला है ?

जो कौमा के इदर और कौमा के इदर वैल्यू बराबर होनी चाहिए मतलब हमें खुद को पहला नच्रूल नबर आपने फूर लेलिया , दूसरा भी फूर ही लेना हैं .

मलब सेल्फ पेर , आप एक तरह से इसको बोल सकते हूँ , सेल्फ जॉयन की तरह हैं , सेल्फ पेर की तरह आपको लेना हैं , दोनो तरभ बराबर एलिमेट .

अब आप इसको साल करो , एक्स मा 2-2 क्या आएगा 0 0 इं teaser के अंदर आती हैं yes , means it is reflexive .

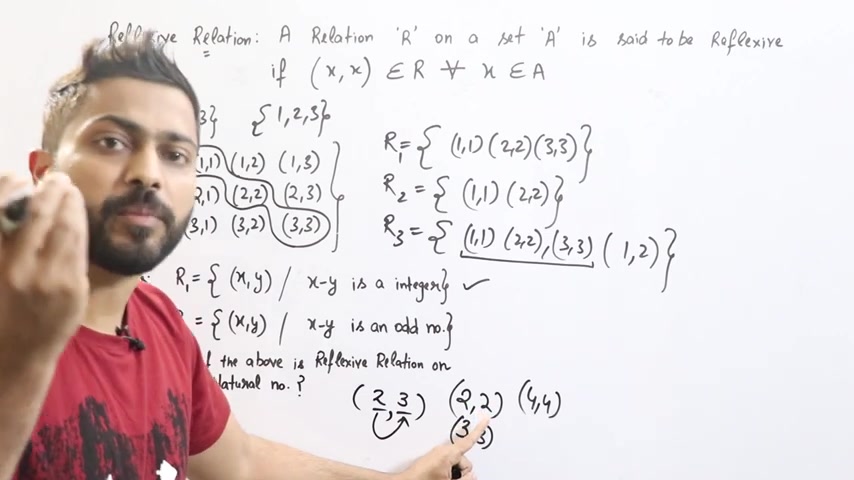
आप कोई मर्जी natural number ले लो कोई मर्जी natural number लोगे और अगर उस number को खुद से ही minus करोगे उसी से minus करोगे तो answer क्या आएगा हमेशा 0 और 0 क्या हैं ?

in teaser तो means it is a reflexive relation .

इस तरीके से आपको check करना ह जाए क्या था ?

जीरो और जीरो नज्रूर नबर के होता नहीं हैं .

तो तब आप कह सकते थे इत इस नॉर्फ्लेक्सिव बड अभी ये रिफ्लेक्सिव हैं .

तइन एक और एजमपल ले लेते हैं .

x , y , x-y एजमपल ले ले ले ले ले .

हमें फिर नज्रूर नबर से � अपने नापर पढ़र पाई नमपर से विठाना हैं। let's say मैंने नटुरा नमबर ले लिए 5 .

getting the point ?

तो दुसरा नमबर कौन सा लूँगा ?

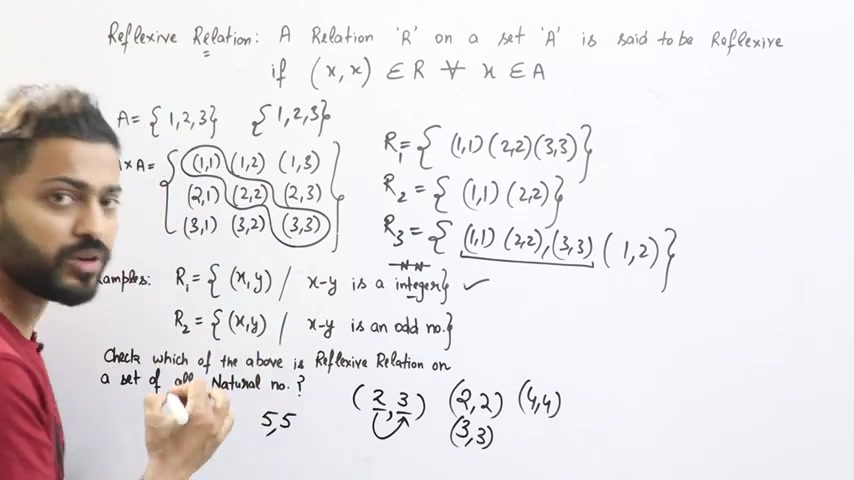
दूसरा नमबर भी 5 लूँगा .

getting the point or not ?

मणब लगा पहला नमबर मैंने 5 ले लिए आ , दुसरा भी 5 लूँगा .

आंसर वाले पेर आने कमपलसरी ही है , तब जाकि आप रेफ्लैकसी बोलोगे .

तो ये जो है हो , इक तरह से मैं आप एक तरह से मैं आपको बतारूँ कि यह यह एर कैसे रिफ्लैक्सिव रिलेशन चेक करते हैं , क्या होता हैं ?

नेक्स्ट वीडियो में हम लोग बात करेंगे कितने रिफ्लैक्सिव रिलेशन पास्सिबल हैं .

थेंकियू .