Statics： Lesson 8 - Intro to 3D Vectors, Deriving Blue Triangle Equations (Spherical Coordinates)

Hey , friends .

Welcome back to the channel .

Today , we're talking about intro to 3 d vectors .

Now we master 2 d vectors .

We're like level 3 experts at that .

It's time to move on to 3 d .

Now the whole goal about the next couple videos , what I'm gonna be talking about , the whole point of it .

Okay ?

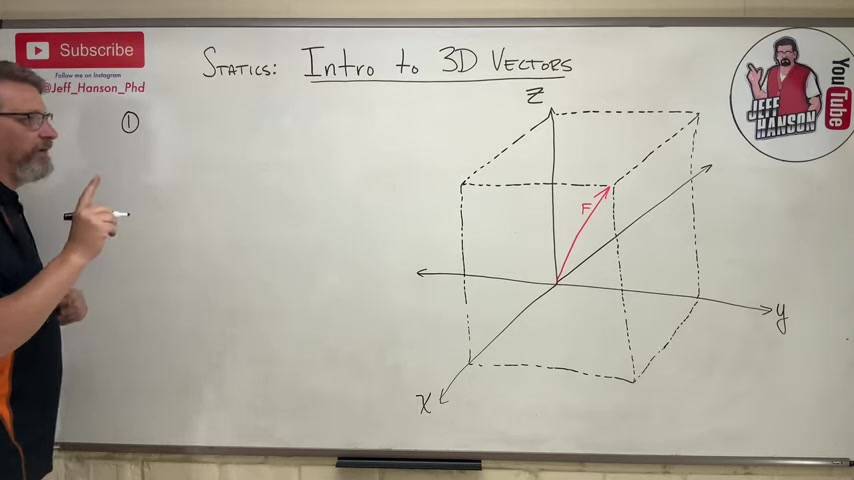
Don't be scared of 3 d because the whole point is just to take a 3 d vector such as this vector here .

K ?

There's some vector .

It goes from the origin to that opposite corner of that cube .

Take that 3 d vector , and we'll call him vector f , and break him into components , I hat , j hat , k hat .

Because if I could take a 3 d vector and break it into I , j , and k , then I can add up a 100 of them .

Right ?

Add all the i's together , add all the j's together , all the k's together .

So everything I'm gonna be doing in the next couple videos is showing you how to take a 3 d vector and make it into I hat , j hat , k n .

That's it .

Okay ?

So don't think , oh , this is gonna be hard .

It's it's not hard .

Okay ?

There are 3 ways , k , that a vector can be expressed in 3 d .

Three ways .

And this , that I'm gonna talk to you on this video , is about way number 1 .

K ?

Number 1 .

And I call this the blue triangle triangle triangle .

Sorry , my speller quit working there in my brain .

Equations .

Okay ?

The blue triangle equations .

Now the reason I call it the blue triangle equations is because in the book , these problems I'm looking for my book .

So in the book , these problems always have or they're expressed with these little blue triangles .

Okay ?

So this particular method , I just call it the blue triangle questions .

You won't find that in the book .

I just I made that up .

Okay ?

So I'm gonna show you how to derive those , how to use them , and you're gonna be like , man , that was so easy .

Okay ?

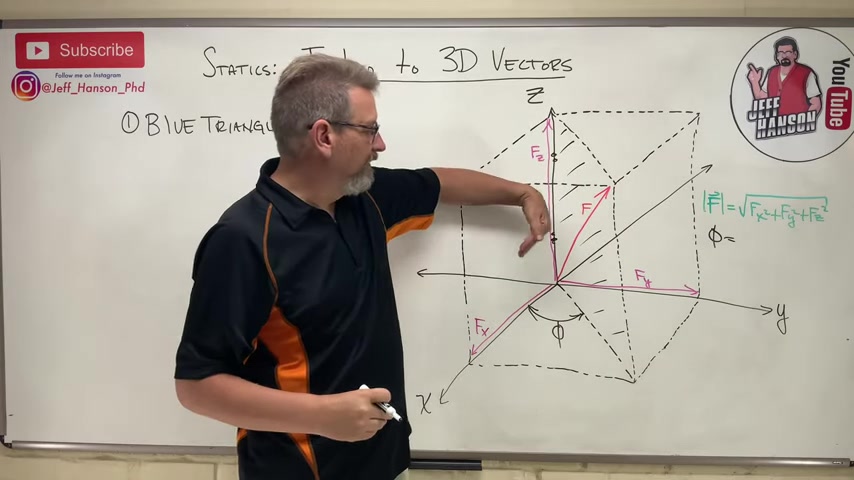
One of the things that I wanna do is I wanna tell you that a 3 d vector , just like a 2 d vector , has projections onto the axes .

Okay ?

So this vector f would have 3 components .

Instead of 2 and 2 d , it has 3 and 3 d .

It has this guy .

Okay .

That's f x .

Has this guy .

That's f y .

And of course it has this guy .

And that's fz .

Okay ?

So that 3 d vector has 3 components .

And the same as it was in 2 d , if I take if I want to know the magnitude of vector f , well , it's the square root of fxsquaredplusfysquaredplusfzsquared .

Okay ?

So find magnitude in 3d the exact same way we do in 2d .

So that's easy to do .

Okay .

Now one of the things I want to kind of tell you about is this , I want to imagine that vector f is contained inside of a plane .

And that plane is right here and right here .

Okay .

So kind of this this plane here , okay .

Imagine that plane as a door .

Okay .

And that door used to be over here on the x axis and it's going and it's opened up .

How much is it opened up ?

It's opened up this much .

Okay .

And we call this angle phi .

Okay .

Angle phi .

Now let me write it over here .

Phi okay .

I call angle phi the swing angle .

Because imagine that as a door and it's hinged , like here's the hinges .

Right ?

There's a hinge here .

There's a hinge here .

Right ?

It's hinged on the z axis and it's allowed to swing .

And it can swing that way or it can swing this way .

It doesn't matter .

But that I call it the swing angle .

And again , don't go looking for that in the book because I just made it up .

Okay ?

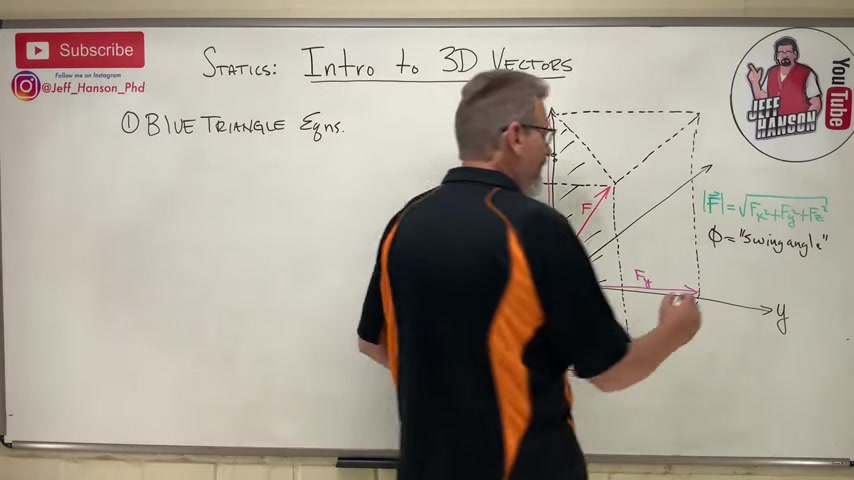
And angle phi is the angle between the positive x axis and the bottom of I'm gonna call it the door .

It's not really the door , but it's the plane .

So and the bottom of the plane , let's call it f h for hypotenuse .

Right ?

This is f h also .

Right ?

That's the hypotenuse of the door .

Okay ?

So that's one angle .

I need one more angle because in 3d in 2d , I could give you a vector and just say , hey , a vector is at 30 degrees and you go , okay , boom , there's 0 and then , well , there's 30 degrees , there's my vector .

Right ?

But in 3 d , I gotta tell you a little more .

I gotta tell you , like , what the inclination is and then I gotta tell you , like , which way it is this way .

Right ?

So phi is the one that tells me where it is this way .

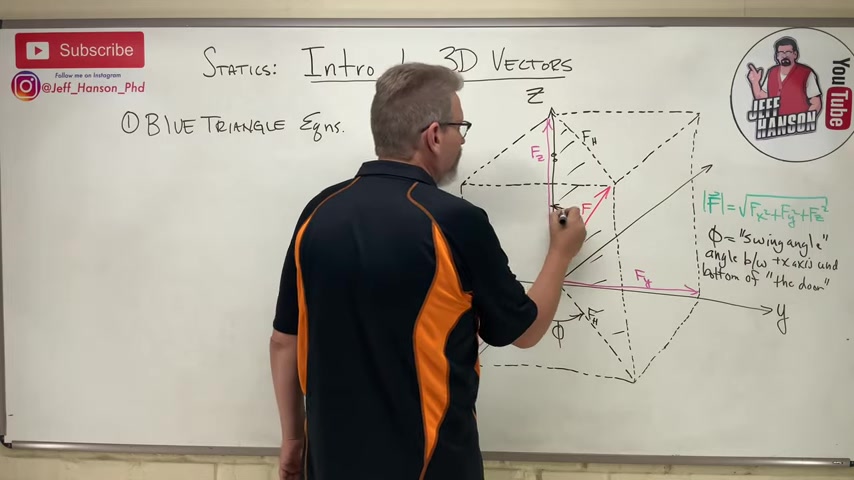
Now I need one that tells me this way .

Right ?

And we call this guy we call this guy theta z .

Okay .

So that's the second angle .

So theta z is the angle between positive z and vector f .

Okay .

So positive z straight up , down .

Okay .

So here's here's theta z is from positive z down to the vector .

Okay .

Now this is the least amount of information that you can possibly have in order to describe a three d vector would be the magnitude , so I need to know how big it is , that would be just f .

And then those two angles , I need to know phi and theta z .

Once I know that , I know the I hat , the j hat , and the k hat every time .

Okay ?

So we're gonna use something called SOHCAHTOA .

Have you ever heard of it ?

We're gonna use a little simple trig and we're gonna derive some equations .

And the goal here is to take that 3 d vector and break them into 3 parts .

F x , f y , and f z .

Right ?

I hat , j hat , k hat .

If I can break it into 3 components like that , dude , I can write it in our Cartesian 4 and I can add 50 of them together .

No problemo .

Okay ?

So step 1 , let's get in a helicopter .

Okay ?

And we're going up here and we're gonna hover straight above this and we're gonna look straight down on that system .

So what would you see if you look straight down that system ?

Well , you would see this .

K .

Here's that y axis .

Here's the x axis .

And here is something .

Okay .

And here is that angle phi right there .

K .

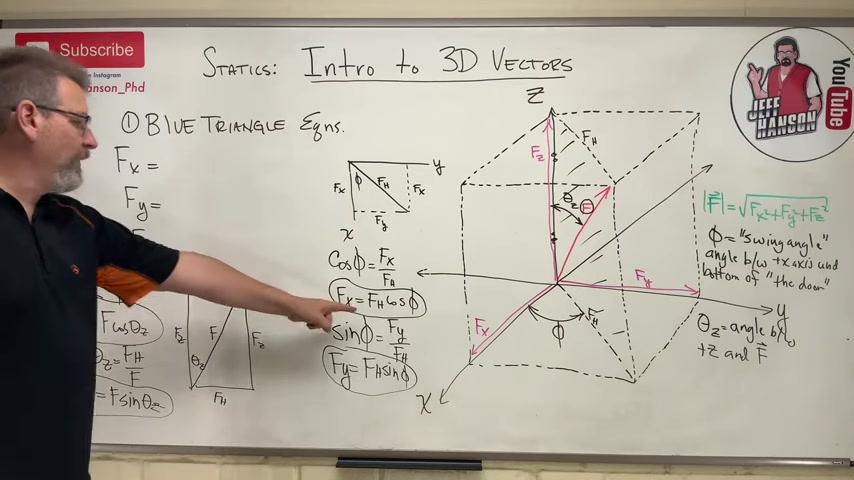
So question and this is , this will be f x and this will be f y .

K ?

Because if this is f x , right , so is that over there .

If this is f y , then so is that over there .

Right ?

Now what am I looking at right here ?

What is that ?

Now I'm in a helicopter looking straight down on it .

Right ?

Johnny Weekes , he would say , oh , that's vector f .

Nuh-uh .

If you were looking straight down on that door , what would you see ?

You'd just see the top of the door , wouldn't you ?

K .

That's actually f h .

K .

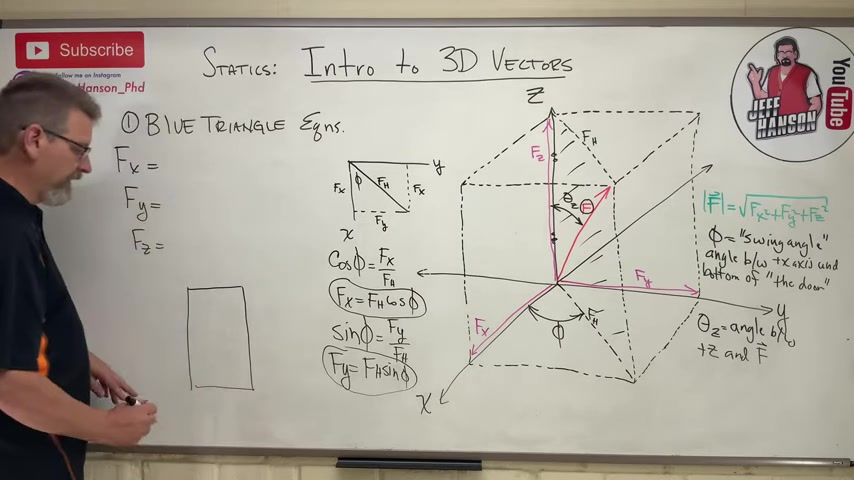
So let's do sine and cosine for this triangle right here .

Okay ?

This is f x over here as well .

K .

So here we go , cosine .

Cosine of phi is equal to opposite ?

No .

No .

That's sine .

Adjacent over hypotenuse , fx over f h .

So we can rearrange that and we can say that fx is equal to fhcosine of phi .

Alright .

Same equation , let's do sine .

Okay .

So sine of phi .

And sine is opposite , boom , over hypotenuse .

So f y over f h .

So let's see f y , we could rearrange this again , f y is equal to f h sine of phi .

Okay ?

So there's 2 little nifty equations for f x and f y .

Alright ?

Let's do one more thing .

Let's look at this door , the plane that contains vector f .

Okay ?

Look at the door .

But let's look at it straight on .

So we're looking straight at the door .

K ?

What would we see ?

Here's the door .

Oh , that's not a very straight line , doctor Hansen .

Okay .

I'll fix it .

Okay .

There's the door .

K ?

Here's vector f right here .

It goes from one corner .

Golly , man .

I'm like king of the crooked lines today , aren't I ?

K .

That's pretty straight .

There's vector f .

K .

The top of the door is f h .

The bottom of the door is f h .

And this is f z .

And this is f z .

And here's theta z .

K ?

I wanna do the exact thing I did over there , little SOH CAH TOA to this triangle right here one more time .

And what am I gonna get ?

Okay .

For this triangle , I get this .

Cosine of theta z is equal to adjacent over hypotamus , so f z over f .

Okay .

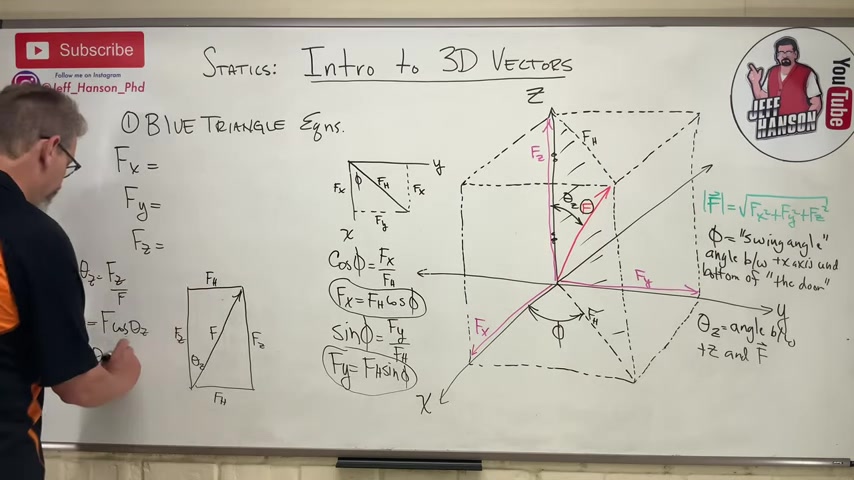
And again , I can rearrange that and I get this , f z is equal to fcosethetaz .

Okay .

And let's do sine .

Sine of thetaz is equal to sine is opposite over above this , so f h over f .

And one more time I can rearrange this guy and I get f h is equal to f sine theta z .

Okay ?

So I have 2 more equations there and there .

Now the overall goal here was to be able to write an fx , an fy , and an fz .

Because if I can get an I j and k , man , I can go to town , yo .

Okay .

So you know what I'm not in love with ?

I'm not in love with f h .

I just want x , y , and z .

I don't need f h in my life , do I ?

K .

So if only I had an equation for f h , that way I could substitute in .

Oh my goodness .

There's one right there .

So let's substitute that in for there .

Okay ?

So f x is equal to f h which is f sine theta z .

K .

And then cosine phi .

K .

And then f y , well he has an f h so I'm gonna substitute again and then sign of and then f z , you know what , f z is okay .

He doesn't have any weird stuff in him so he's just f cos theta z .

Okay .

Boom .

We just did it y'all .

We just did it .

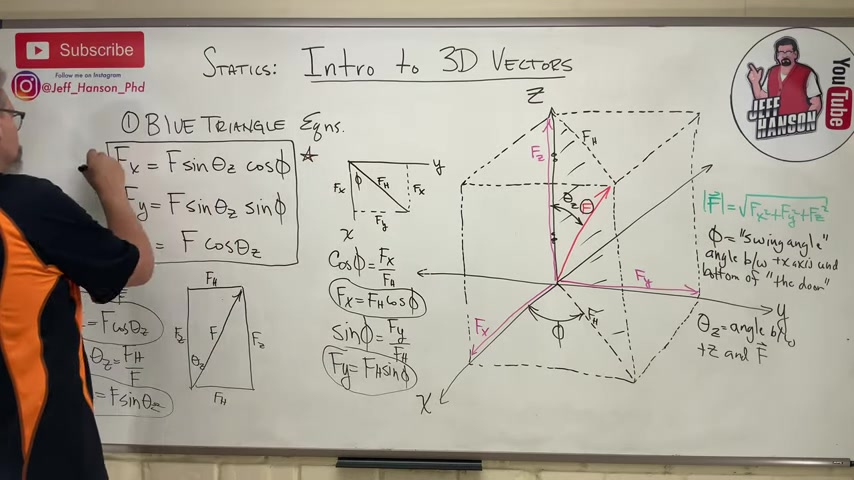
Now that one really hard because all we used was SOHCAHTOA , but you should put a star by that .

K .

Those are the blue triangle equations .

Okay ?

Those are the blue triangle equations .

Those are the ones that you should remember and , helpful on the test to remember that .

Okay ?

These are the blue triangle equations .

Alright ?

So what do you need to use the blue triangle equations ?

What do you need ?

Well , you need to look at one of those blue triangle problems and you need to identify 3 things .

Number 1 , what is f ?

Which is generally given .

They'll tell you , hey , the magnitude of this vector is 300 newtons or something like that .

Right ?

That's pretty much given .

What is phi ?

Okay .

Well , you all you have to do is remember , what was phi ?

Oh , yeah .

It's the swing angle .

It's the angle between the positive x axis in and the bottom of the door .

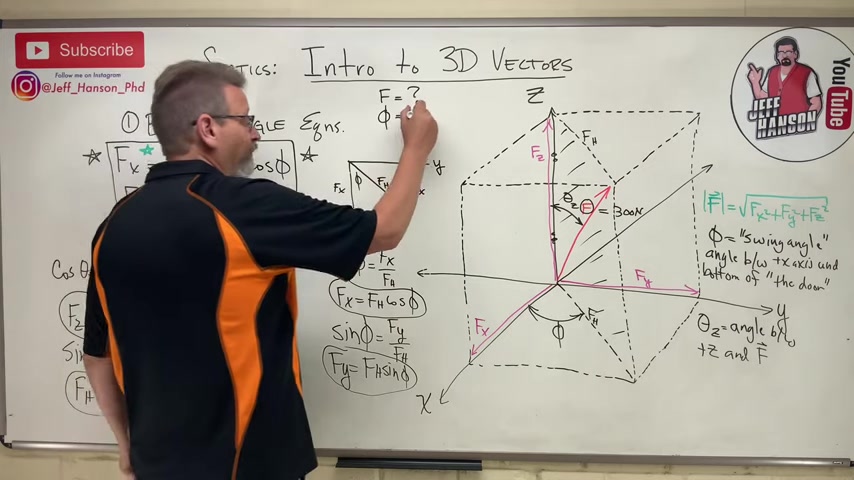
And if you can find that angle , dude , all you gotta do is plug it into these equations .

So phi equals what ?

And then finally , what does theta z equal ?

Right ?

So if I and and there it is , from positive z down to the vector .

So if I can identify those three things , I can plug them into those three equations and then just solve them .

I just turn the crank in my calculator .

Right ?

And I'm done .

Here's the deal that is nice about these equations .

Okay ?

Number 1 , they just came from SoCoteau .

Number 2 is if you put the right thing in these equations , it will give you the right sign out .

Okay ?

Because you can look at a vector .

Like this vector here , I can see has a positive x , a positive y , and a positive z .

So when I put my stuff in these equations , I'm gonna get a positive , a positive , and a positive .

If I don't , if the calculator gives me a negative for one of these , then I did something wrong .

Now here's the other thing .

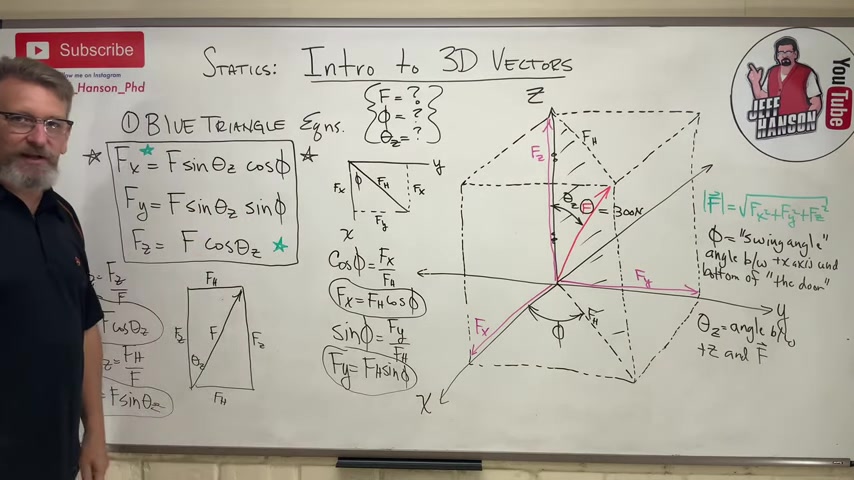
On the other hand , if you put garbage in for these variables , right , if you put garbage into those equations , guess what you're gonna get out ?

Garbage .

Okay .

So that's how that's where they come from .

The the main thing is I want you to do you'll be able to do is identify what is fee , what is state of z .

Okay ?

In the next video , what I'm gonna do is I'm gonna put a whole bunch of those up here on the board , and I'm gonna drill you over it .

Okay ?

I'm gonna ask you over and over .

What's fee ?

What's state of z ?

And you're gonna push pause and you're gonna tell me .

Okay ?

So I'm gonna drill you on this because once you can start identifying what is phi and what is saying to z , how easy is this ?

Just plug it in .

Put it in your calculator .

Done .

Right ?

Easy .

I hat , j hat , k hat .

Okay ?

So get ready for some exercise .

I'm fixing to drill you on some , on some problems .

Hang on .